火车过桥问题

【慕联导读】

慕联导读（简介）：

火车过桥问题是行程问题的一种，也有路程、速度与时间之间的数量关系，同时还涉及车长、桥长等问题。

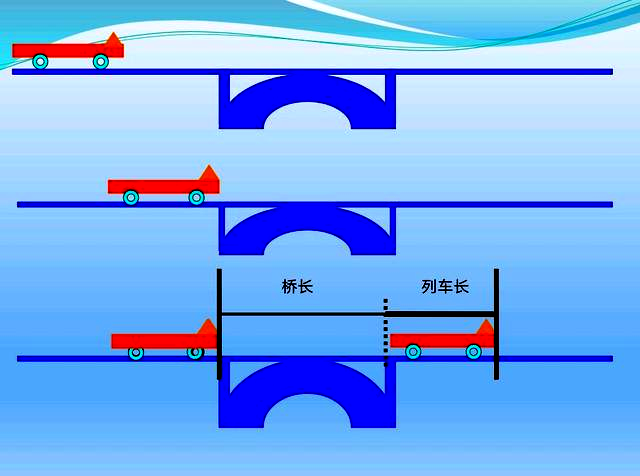
人过桥，由于不考虑人的宽度，从人上桥到下桥，所行路程就是桥的长度，是普通的行程问题，但火车过桥就不一样，火车有长度，从火车头接触桥头开始，到火车尾正好离开桥尾为止，所行路程为桥长+车长。

  过桥问题是行程问题的一种情况。我们所说的列车通过一座桥，是指从车头上桥到车尾离桥的这个过程。这时，列车行驶的总路程是桥长加上车长，这是解决过桥问题的关键。

  过桥问题也是在研究路程、速度、时间这三量之间的关系。

一、基本介绍

过桥问题的一般数量关系：

    路程=桥长+车长

    车速=（桥长+车长）÷通过时间

    通过时间=（桥长+车长）÷车速

    桥长=车速×通过时间－车长

    车长=车速×通过时间－桥长

通过隧道的问题和过桥问题的道理是一样的，也要通过上面的数量关系来解决。

重点：把握火车走的路程为桥长加车长

类型：

1、火车过桥：火车+有长度的物体

  S=桥长+车长    解法：S=火车速度×通过时间

2、火车+人

（1）、火车+迎面行走的人，相当于相遇问题

    S=车长    解法：S=（火车速度+人的速度）×迎面错过的时间

（2）、火车+同向行走的人，相当于追及问题

    S=车长    解法：S=（火车速度-人的速度）×追及时间

3、火车+车

（1）、错车问题，相当于相遇问题

S=两车车长之和，解法：S=（快车速度+慢车速度）×错车时间

（2）、超车问题：相当于追及问题

S=两车车长之和，解法：S=（快车速度-慢车速度）×错车时间

4、火车上人看车从身边经过

（1）、看见对车从身边经过，相当于相遇问题

S=对车车长，   解法：S=两车速度之和×相遇时间

（2）、看见后车从身边经过（相当于追及问题）

S=后车车长，解法：S=两车速度之差×经过时间

注意事项：

1、画图

2、分清方向和位置

3、单位统一

二、例题解析

例1. 一列火车经过南京长江大桥，大桥长6700米，这列火车长140米，火车每分钟行400米，这列火车通过长江大桥需要多少分钟？

分析：这道题求的是通过时间。根据数量关系式，我们知道要想求通过时间，就要知道路程和速度。路程是用桥长加上车长。火车的速度是已知条件。

    总路程：6700+140=6840 （米）

    通过时间：6840÷400=17.1 （分钟）

    答：这列火车通过长江大桥需要17.1分钟。

例2. 一列火车长200米，全车通过长700米的桥需要30秒钟，这列火车每秒行多少米？

分析：这是一道求车速的过桥问题。我们知道，要想求车速，我们就要知道路程和通过时间这两个条件。可以用已知条件桥长和车长求出路程，通过时间也是已知条件，所以车速可以很方便求出。

    总路程：200+700=900（米）

    火车速度：900÷30=30（米/秒）

    答：这列火车每秒行30米。

例3. 一列火车长240米，这列火车每秒行15米，从车头进山洞到全车出山洞共用20秒，山洞长多少米？

分析：火车过山洞和火车过桥的思路是一样的。火车头进山洞就相当于火车头上桥；全车出洞就相当于车尾下桥。这道题求山洞的长度也就相当于求桥长，我们就必须知道总路程和车长，车长是已知条件，那么我们就要利用题中所给的车速和通过时间求出总路程。

    总路程： 15×20=300（米）

    山洞长： 300-240=60（米）

    答：这个山洞长60米。

例4. 一列火车通过360米的第一个隧道用了24秒钟，接着通过第二个长216米的隧道用了16秒钟，求这列火车的长度。

分析：这道题让我们求火车的长度。我们知道：车长＝车速×通过时间－隧道长。其中“通过时间”和“隧道长”都是已知条件。我们就要先求出这道题的解题关键：车速。通过审题我们知道这列火车通过不同长度的两个隧道用了不同的时间。所以我们可以利用这两个隧道的长度差和通过时间差求出车速。

    车速：（360-216）÷（24-16）=18（米）

    火车长度：18×24-360=72（米）

    或 18×16-216=72（米）

    答：这列火车长72米

例5. 某列车通过342米的隧道用了23秒，接着通过288米的隧道用了20秒，这列火车与另一列长128米、速度为22米的列车错车而过，问需要几秒钟？

分析：这道题结合了过桥问题与相遇问题两种知识。

   要求错车而过的时间，就要知道两列火车的长度和速度。

   第二列火车的长度和速度是已知的，所以求第一列火车的长度和速度就是解题的关键。

    第一列火车速度：

（342-228）÷（23-10）=18（米）

    第一列火车长度：18×23-342=72（米）

    或 18×20-288=72（米）

    错车时间：（72+128）÷（22+18）=5（秒）

    答：两列火车错开而过需要5秒钟。

例6. 一位旅客乘火车以每秒15米的速度前进，他看见对面开来的火车只用2秒钟就从他身边驶过。如果知道迎面来的火车长70米，求它每小时行驶多少千米？

分析：请同学们认真审题，别受误导。

这道题与上一道题有着本质的不同。这道题是以这个旅客为标准，第二列火车从车头到车尾从他身边经过用了2秒钟，也就是70米长用2秒钟走完。而这个过程的速度是两列火车的速度和。

    速度和：70÷2=35（米）

    火车速度：35-15=20 （米）

    答：迎面而来的火车每小时行驶20千米。

例7．慢车车长为125米，车速为17米/秒，快车车长140米，车速为22米/秒，慢车在前面行驶，快车在后面追上到完全超过需要多少时间？

分析：属于火车过桥问题中的超车问题。快车追及的路程差应为快车的车长加慢车的车长（画图）

（125+140）÷（22-17）=53秒

例8．小明坐在行驶的车上，从窗外看到迎面开来的货车经过用了6秒，已知货车长168米；后来又从窗外看到列车通过一座180米的桥用了12秒，货车的速度是多少？

分析：前半句话，是相遇问题，相遇路程为货车车长，168÷6=28米/秒，即为列车和货车的速度和。

后半句话：路程为桥长，（注意与人站在路边看火车从身边经过的路程区分开）

180÷12=15米/秒，即为火车的车速，那货车的车速就为28-15=13米/秒

例9．（部队过桥）一支队伍长1200米，在行军。在队尾的通讯员用了6分钟跑到队最前的营长联系，为了回到队尾，他在追上营长的地方等了24分钟后，如果他是跑出队尾，只要多长时间？

分析：追上营长，是一个追及问题，追及路程就是队伍的长度，我们就可以求出速度差是：1200÷6=200米/分。后句话，通讯员在等，实质是一个火车过桥问题（车+无长度物体）

S=队伍长=1200米，那么，队伍的速度就是：1200÷24=50米/分。所以通讯员的速度就是：200+50=250米/秒。如果他跑回队尾，实质是相遇问题，S=队伍长=1200米，时间就可以求出来了，相遇时间=1200÷（250+50）=4分钟。