七桥问题

【慕联导读】

欧拉回路关系:

如果一个图形可以一笔画出来，则必须满足两个条件：

（1）图形必须是连通的，即任一点通过一些线一定能达到其他任意点。

（2）图中的奇点数只能是0或2.

一、 七桥漫步

格尼斯堡城是由条顿骑士团在1308年建立，曾作为东普鲁士的首府。第二次世界大战后，成为前苏联最大的海军基地。现在的格尼斯堡位于立陶宛和波兰之间。在第二次世界大战时，法军经这里入侵波兰。后来苏军也从这里打进德国，所以格尼斯堡是一座名城。同时这里也诞生过许多伟大人物，其中包括18世纪著名的唯心主义哲学家康德和19世纪的大数学家希尔伯特。

但是，最早给这座城市带来声誉的横跨布列格尔河，把格尼斯堡连成一体的七座桥梁。

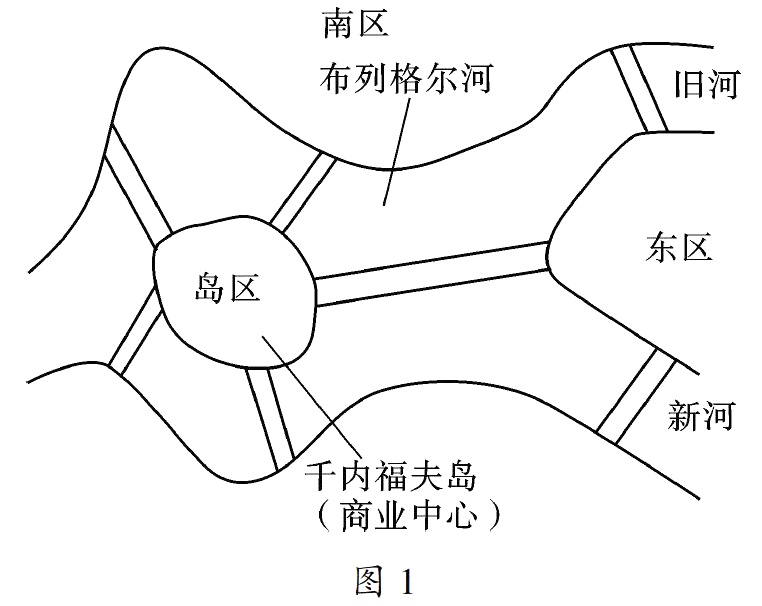
这一别致的桥群，引来了众多的游人，同时还引发了数学史上一项重要的研究。

一天又一天，这七座桥上走过了无数的行人，脚下的七桥触发了人们的灵感，一个有趣的问题在民间传开“能否在一次散步中每座桥都走一次，而且只能走一次，最后又回到原来的出发点？”这个问题看似简单，人人都乐意去测试一下自己的智力，可是把全城人的智力加在一起，也没有找到一条合适的路线。这个问题传开以后，许多欧洲有学问的人也参与思考，同样是一筹莫展。就这样，格尼斯堡这个“七桥问题”给人们提供了丰富的乐趣和数学兴味，因而使得这座波罗的海的海滨古城闻名遐迩。

二、欧拉与格尼斯堡七桥问题

1735年有几名大学生写信给当时正在俄国彼得堡科学院任职的天才数学家欧拉，请他帮助解决。欧拉并未轻视生活中的小问题，他似乎看到了其中隐藏某种新的数学方法。

事实上，要走遍七座桥的所有走法有7！=5040种，要想一一试验是不可能的，只能另找一种新方法。欧拉依靠他深厚的数学功底，运用娴熟的变换技巧，经过一年的研究，于1936年，29岁的欧拉向彼得堡科学院提交了一份为《格尼斯堡七桥》的论文，圆满的解决了这一问题。欧拉不仅解决了七桥问题，而且他提出飞思想导致了一门新的数学分支——“图论”的诞生。

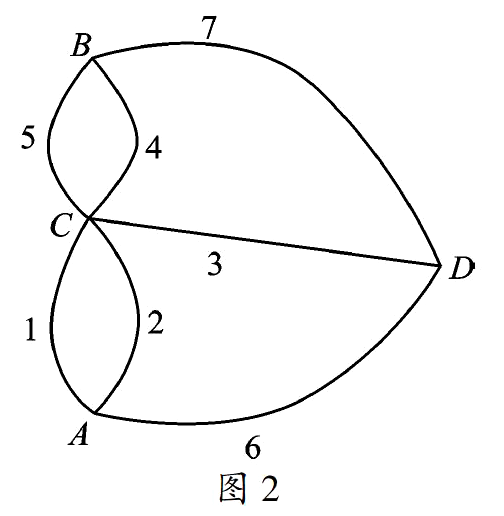
 欧拉是如何解决七桥问题的？又是如何证明要想一次走过七座桥是不可能的呢？欧拉的方法十分巧妙：（1）不考虑4个地区的大小、形状，不妨将它们看成是链接桥梁的4个点；

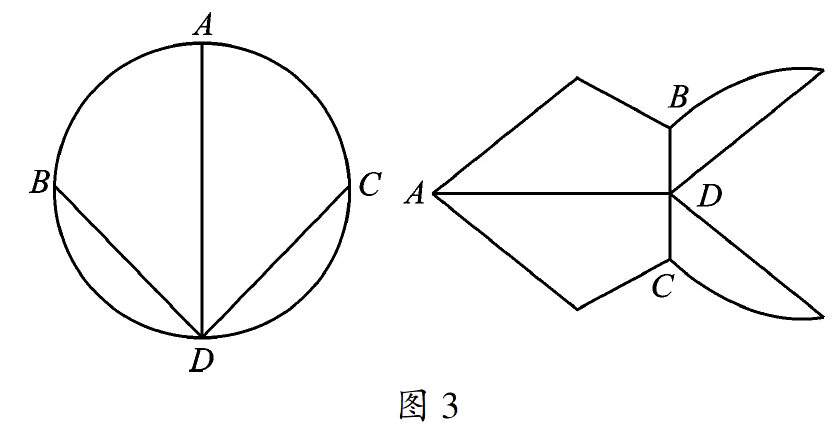
（2）不考虑桥梁的曲直、长短，不妨将它们看成连接4个点的7条线。

 于是一座仪态万千的格尼斯堡古城在欧拉笔下就变成了一个结构简单是几何图形。

1736年，在经过一年的研究之后，29岁的欧拉提交了《哥尼斯堡七桥》的论文，圆满解决了这一问题，同时开创了数学新一分支---图论。

于是七桥问题就变成了用笔不重复的（笔不离开纸面）画出这个几何图形的问题，即“一笔画”问题。如果可以画出来，则必有一个起点和一个终点，如果这两点不重合，则与起点或终点相交的线必为奇数条（称为奇点），如果起点与终点重合，则与之相交的线必为偶数条（称为偶点），而除了起点与终点外，其他点也必为偶点。据以上分析，如果一个图形可以一笔画出来，则必须满足两个条件：

（1）图形必须是连通的，即任一点通过一些线一定能达到其他任意点。

（2）（2）图中的奇点数只能是0或2.

回头来看七桥问题，4个点全为奇点，故七桥问题无解。欧拉当时发表这一结果时，震惊了当时的数学界。

欧拉通过对七桥问题的研究，不仅圆满地回答了哥尼斯堡居民提出的问题，而且得到并证明了更为广泛的有关一笔画的三条结论，人们通常称之为欧拉定理。对于一个连通图，通常把从某结点出发一笔画成所经过的路线叫做欧拉路。人们又通常把一笔画成回到出发点的欧拉路叫做欧拉回路。具有欧拉回路的图叫做欧拉图。

来源：互联网     编辑：黄桂艳