十字相乘法

【慕联导读】

十字分解法的方法简单来讲就是：十字左边相乘等于二次项，右边相乘等于常数项，交叉相乘再相加等于一次项。其实就是运用乘法公式(x+a)(x+b)=x²+(a+b)x+ab的逆运算来进行因式分解。

（1）对于二次项系数为1的二次三项式x²+(a+b)x+ab=(x+a)(x+b)

方法的特征是“拆常数项，凑一次项”

当常数项为正数时，把它分解为两个同号因数的积，因式的符号与一次项系数的符号相同；当常数项为负数时，把它分解为两个异号因数的积，其中绝对值较大的因数的符号与一次项系数的符号相同。

例1：因式分解x²-x-56

例2：因式分解x²-10x+16

（2）对于二次项系数不是1的二次三项式ax²+bx+c=a₁a₂x²+(a₁c₂+a₂c₁)x+c₁c₂=

(a₁x+c₁)(a₂x+c₂)

方法的特征是“拆两头，凑中间”

当二次项系数为负数时，先提出负号，使二次项系数为正数，然后再看常数项；常数项为正数时，应分解为两同号因数，它们的符号与一次项系数的符号相同；常数项为负数时，应将它分解为两异号因数，使十字连线上两数之积绝对值较大的一组与一次项系数的符号相同。

注意：用十字相乘法分解因式，还要注意避免以下两种错误出现：一是没有认真地验证交叉相乘的两个积的和是否等于一次项系数；二是由十字相乘写出的因式漏写字母。

例3：因式分解6y²+19y+15

分析：该题虽然二次项系数不为1，但也可以用十字相乘法进行因式分解。

例4：因式分解10(x+2)²-29(x+2)+10

分析：该题可以将(x+2)看作一个整体来进行因式分解。

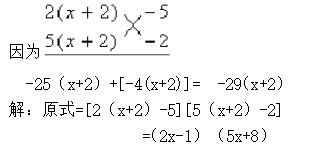
从上面几个例子可以看出十字相乘法对于二次三项式的分解因式十分方面，大家一定要熟练掌握。但要注意，并不是所有的二次三项式都能进行因式分解，如x²-2x+5在实数范围内就不能再进一步因式分解了。

来源：互联网     编辑：徐慧芳