斐波纳契数列

【慕联导读】

在中世纪的意大利，有一位“最有才华的西方数学家”，名叫列奥纳多·皮萨诺。是他率先将阿拉伯数字和乘数的位值表示法系统引入了欧洲。但现在人们提到他的时候经常称其为斐波纳契。这是怎么回事呢？原来他在1202年出版了《计算之书》一书，在书中他列举了斐波那契数列，这个数列太知名了，所有后人常以“斐波那契”来称呼他。

在《计算之书》中，作者介绍了斐波那契研究的一个数学问题——兔子在理想环境下繁殖的速度。假设一对新生的兔子，一只公的，一只母的，被放进田里豢养。兔子可以在一个月大的时候交配，这样在第二个月的月底，雌性兔子就能生产出另一对兔子。假设兔子永远不会死，从第二个月开始，雌兔每个月都会生一对新的兔子（一雄一雌）。斐波那契提出的问题是：一年后总共会有多少对兔子？

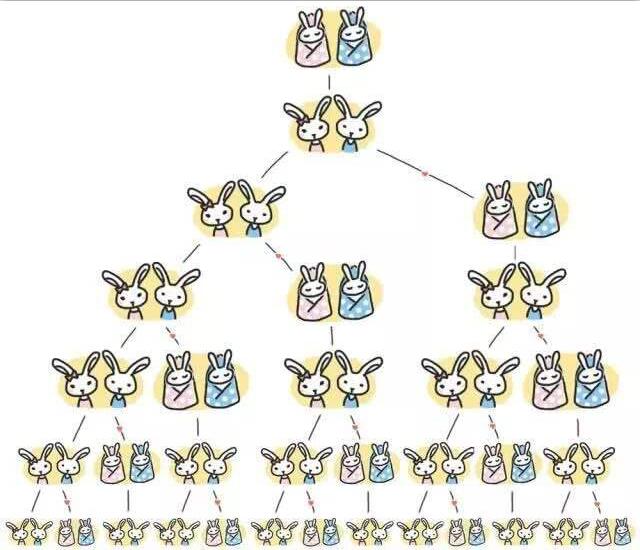
 这个问题的背后，就是著名的斐波那契数列：0，1，1，2，3，5，8，13……，产生斐波那契数列的规则是：前两项数字相加的和为下一项的数字。用公式表示就是：x_n+1=x_n+x_n-1。

 兔子的问题是人为设立出来的，在自然界中，体现这一数学规律的情况还是很多的，蜜蜂就是其中的一例。蜜蜂中的雄蜂是由蜂王的未受精卵子产生的，所以说它只有母亲而没有父亲。而雌蜂是在蜂王和一只雄性交配的时候产生的，因此雌蜂有父母。如果将它们的家谱从下往上看，就会发现，无论是雄蜂还是雌蜂，其代际之间的数量关系，都遵循斐波那契数列，其中雄蜂是1，2，3，5，8……，雌蜂是2，3，5，8，13……。

 海螺那美丽的螺旋形状的背后，同样隐含着斐波那契数列。我们可以从两个叠在一起的边长为1的小正方形开始，然后画一个边长为2的正方形紧贴此前画好的两个小正方形；接下来画一个边长为3的正方形紧贴此前已经画好的图形……就这样继续在图片周围添加正方形，每一个新的正方形都有一个边，其长度与最近两个正方形的边之和一样长。如果在每个正方形上画一个四分之一的圆，并将这些圆弧依次连接起来，就会看到这根曲线非常近似于经常出现在自然界中的螺旋形状，比如蜗牛和贝壳的形状。

 不光是动物中包含着这样的神奇的数学，植物花瓣的数量通常也都是斐波纳契数列中的数字。比如：延龄草有3瓣花瓣，紫罗兰有5瓣，飞燕草有8瓣，万寿菊有13瓣，菊苣有21瓣，除虫菊有34瓣，向日葵则通常有55甚至89瓣。也有一些植物的花瓣的数量是斐波纳契数列中的数字的二倍，比如某些品种的百合，其花朵由两朵花组合而成。知道了花瓣中蕴含的这奇妙的数字，你找时间可以仔细去数一数，如果花瓣的数量不符合斐波纳契数列中的数字，那么一定是有花瓣掉落下来了。

 如果你仔细观赏向日葵的花盘以及种子的排列，你还会先种子特别神奇、美丽的排列方式，它们是两组螺旋线，一组顺时针向右，一组逆时针向左，并且彼此镶嵌。当你从中央逐渐向花盘的边缘看过来的时候，你可以看到55个左旋的螺旋线，如果你盯着同一点看，还可以看到左边有34个螺旋，右边有21个螺旋。这些数字，都隐含在斐波那契数列之中。

 除花朵以外，在松果和菠萝上也可以发现斐波纳契数列中的数字。切开一只香蕉，你就会发现它是由三个部分组合而成的。而从一个苹果的茎部一刀切至底部，你就能看到一个五角星的形状。如果切开一个莎隆果，你就能看到一个八角星的形状。

 列奥纳多•皮萨诺是如何发现这一数列的呢？据说与中世纪印度的诗人和音乐家有关。公元8世纪，印度作家维拉汉卡决定接受挑战，探索一下到底有多少种不同的节奏存在。他发现随着节拍数量的增加，可能的节奏模式的数量会按照以下序列依次增加：1，2，3，5，8，13……。他也意识到，要得到数列中的后一个数字，只需将前面的两个数字相加即可。于是，当我们想知道8个节拍中有多少种节奏的可能性时，只需查看序列中的第8个数字即可，即由13和21相加所得来的34，因此，8个节拍中共有34种不同的节奏组合。

来源：互联网     编辑：沈新悦