韦达定理

【慕联导读】

韦达定理说明了一元二次方程中根和系数之间的关系。

法国数学家弗朗索瓦·韦达在著作《论方程的识别与订正》中建立了方程根与系数的关系，提出了这条定理。由于韦达最早发现代数方程的根与系数之间有这种关系，人们把这个关系称为韦达定理。

一、定理关系：

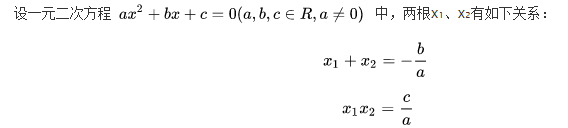
二、数学推导：

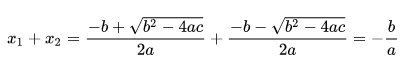
三、定理推广：

1.逆定理：

如果两数α和β满足如下关系：α+β=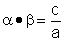，，那么这两个数α和β是方程

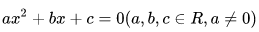的根。

通过韦达定理的逆定理，可以利用两数的和积关系构造一元二次方程。

2.推广定理：

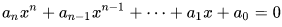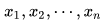设复系数一元n次方程的根为，则成立

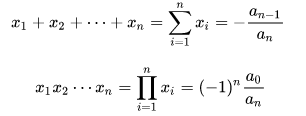
即：所有根之和为（n-1）次项系数与n次项系数之比的相反数，所有根之积为常数项与n次项系数之比再乘以（-1）ⁿ

注：该推广形式的证明一般无法根据求根公式进行，因为5次以上的一元方程没有求根公式。证明步骤较繁琐，是通过将左边的多项式因式分解成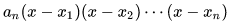之后，再去括号，比较相同次数的项的系数从而得出结论。这个方法具有普遍性，即使是有求根公式的方程，亦可以通过该方法证明韦达定理，而无需借助求根公式。

四、发展简史

法国数学家弗朗索瓦·韦达在著作《论方程的识别与订正》中改进了三、四次方程的解法，还对n=2、3的情形，建立了方程根与系数之间的关系，现代称之为韦达定理。

韦达最早发现代数方程的根与系数之间有这种关系，因此，人们把这个关系称为韦达定理。韦达在16世纪就得出这个定理，证明这个定理要依靠代数基本定理，而代数基本定理却是在1799年才由高斯作出第一个实质性的论性。

弗朗索瓦·韦达

五、定理意义

韦达定理在求根的对称函数，讨论二次方程根的符号、解对称方程组以及解一些有关二次曲线的问题都凸显出独特的作用。

一元二次方程的根的判别式为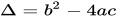（a，b，c分别为一元二次方程的二次项系数，一次项系数和常数项）。韦达定理与根的判别式的关系更是密不可分。

根的判别式是判定方程是否有实根的充要条件，韦达定理说明了根与系数的关系。无论方程有无实数根，实系数一元二次方程的根与系数之间适合韦达定理。判别式与韦达定理的结合，则更有效地说明与判定一元二次方程根的状况和特征。 

韦达定理最重要的贡献是对代数学的推进，它最早系统地引入代数符号，推进了方程论的发展，用字母代替未知数，指出了根与系数之间的关系。韦达定理为数学中的一元方程的研究奠定了基础，对一元方程的应用创造和开拓了广泛的发展空间。 

利用韦达定理可以快速求出两方程根的关系，韦达定理应用广泛，在初等数学、解析几何、平面几何、方程论中均有体现。

来源：互联网     编辑：沈新悦