杨辉三角

【慕联导读】

杨辉三角，是二项式系数在三角形中的一种几何排列。在欧洲，这个表叫做帕斯卡三角形。帕斯卡（1623----1662）是在1654年发现这一规律的，比杨辉要迟393年，比贾宪迟600年。杨辉三角是中国古代数学的杰出研究成果之一，它把二项式系数图形化，把组合数内在的一些代数性质直观地从图形中体现出来，是一种离散型的数与形的结合 。

幻方，在我国也称纵横图，它的神奇特点吸引了无数人对它的痴迷。从我国古代的“河出图，洛出书，圣人则之”的传说起，系统研究幻方的第一人，当数我国古代数学家——杨辉。

    杨辉，字谦光，钱塘(今杭州)人，我国南宋时期杰出的数学家，与秦九韶、李冶、朱世杰并称宋元四大数学家，他在我国古代数学史和数学教育史上占有十分重要的地位。 
    杨辉对幻方的研究源于一个小故事。当时杨辉是台州的地方官，一次外出巡游，碰到一孩童挡道，杨辉问明原因方知是一孩童在地I 做一道数学算题，杨辉一听来了兴趣，下轿来到孩童旁问是什么算题。原来，这个孩童在算一位老先生出的一道趣题：把1到9的数字分行排列，不论竖着加、横着加，还是斜着加，结果都等于15。 
    杨辉看到这个算题时想起来他在西汉学者戴德编纂的《大戴礼》一书中也 
见过。杨辉想到这儿，和孩童一起算了起来，直到午后，两人终于将算式摆出来了。 
    后来，杨辉随孩童来到老先生家里，与老先生谈论起数学问题来。老先生说：“北周的甄弯注《数术记遗》一书中写过‘九宫者，二四为肩，六八为足，左三右七，戴九履一，五居中央。”’杨辉听了，这与自己与孩童摆出来的完全一样。便问老先生：“你可知这个九宫图是如何造出来的?”老先生说不知道。

    杨辉回到家中，反复琢磨。一天，他终于发现一条规律，并总结成四句话：“九子斜排，上下对易，左右相更，四维挺出”。就是说：先把l～9九个数依次斜排，再把上l下9两数对调，左7右3两数对调，最后把四面的2、4、6、8向外面挺出，这样三阶幻方就填好了。

    杨辉研究出三阶幻方(也叫络书或九宫图)的构造方法后，又系统的研究了四阶幻方至十阶幻方。在这几种幻方中，杨辉只给出了三阶、四阶幻方构造方法的说明，四阶以上幻方，杨辉只画出图形而未留下作法。但他所画的五阶、六阶乃至十阶幻方全都准确无误，可见他已经掌握了高阶幻方的构成规律。

“杨辉三角”中数的排列规律：每一行两端都是1，其余各数都是上一行中与数最相邻的两数之和，如

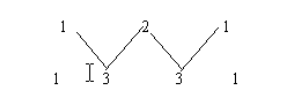
这个数表是南宋数学家杨辉收录在他的著作里才流传下来的。据他的著作里记载，这个数表早在11世纪由北宋数学家贾宪所发现。因此，后人把“杨辉三角”称为“贾宪三角”。

在西方，称这个数表为“帕斯卡三角形”。帕斯卡在1653年开始应用这个三角形数表，发表则在1655年。这就是说，就发现和应用这个三角形而言，贾宪比帕斯卡早600年左右，杨辉比帕斯卡早400年。

与杨辉三角联系最紧密的是二项式乘方展开式的系数规律，即二项式定理。例如在杨辉三角中，第3行的三个数恰好对应着两数和的平方的展开式的每一项的系数，第4行的四个数恰好依次对应两数和的立方的展开式的每一项的系数，即

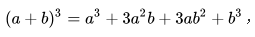
以此类推。

第n行的m个数可表示为C(n-1,m-1)，即为从n-1个不同元素中取m-1个元素的组合数。因此可得出二项式定理的公式为：

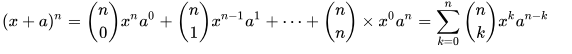
因此，二项式定理与杨辉三角形是一对天然的数形趣遇，它把数形结合带进了计算数学。求二项式展开式系数的问题，实际上是一种组合数的计算问题。用系数通项公式来计算，称为“式算”；用杨辉三角形来计算，称作“图算” 。

来源：互联网     编辑：徐慧芳