折纸中的数学

【慕联导读】

折纸，通常意义上的儿童游戏，居然可以运用到数学、天文学、医学等多个高精行业，这一切，是怎样发生的？又是怎样的一些人，让这看似不可能的一切发生了？

折纸问题中的数学

通过折纸活动，分析留在纸张上的折痕，我们能够揭示出大量几何的对象和性质：轴对称、中心对称、全等、相似形、比例及类似于几何分形结构的迭代 (在图案内不断地重复图案 )等几何性质。

折纸过程还能够体现出许多几何概念和规律，诸如正方形、矩形、直角三角形、梯形等几何形状，对角线、中点、垂直平分线等几何名称，全等、勾股定理等几何法则，内接、面积及其他一些几何代数的概念，这些鲜活的、可视的过程，给学生提供了弥补思维过程中的断缺部分，更能符合学生的认知习惯。

折纸可以探索二维和三维图形之间的关系。例如，一张正方形 (二维物体 )的纸张可以折成一个立方体 (三维物体 )。然后，将它摊开 ,研究留在正方形纸上的折痕，正好体现了一个二维物体到三维物体，又回到二维的过程。

在缤纷多彩的折纸活动中，有很多数学活动值得研究。在这里，我们精选了其中的一些，展示如下：

（ 1）从一个矩形式样的纸张 ,折成一个正方形 (如图 2.2-15所示 )。

（ 2）将一张正方形的纸沿着对角线对折 ,变成四个全等的直角三角形 (如图 2.2-16所示 )。

（ 3）找出正方形一条边的中点 (如图 2.2-17所示 )。

（ 5）将一个正方形纸张折叠 ,使折痕过正方形中心，便会构成两个全等的梯形 (如图 2.2-19所示 ) 。

（ 6）把一个正方形折成两半，那么，折痕将成为正方形两条相对边的垂直平分线 (如图 2.2-20所示 ) 。

（ 7）折出四面体 (按图 2.2-21所示的方法 ) 。

（ 8）折出正方体 (按图 2.2-22所示的方法 ) 。

不仅如此，折纸还可以做出其他的一些重要内容，诸如黄金比等。

（ 9）折出黄金分割比

图 2.2-24所展示的是在长方形纸片的一条边中点折出 60°角的方法： 将一张矩形的纸沿两条较短的边（即宽）对折，折出这张矩形纸的平行于较长边的中线，再将这张纸铺平；用手捏住矩形的一个角，将同一条宽上的另一个顶点折向中线，使其刚好落在中线上，压平。

此时，左上角的 90°角就分成了三个 30°角。

利用图 2.2-24中的 60°角，借助于顶角为 60°的等腰三角形是正三角形，通过连续折叠四个正三角形，还可以做出正四面体。

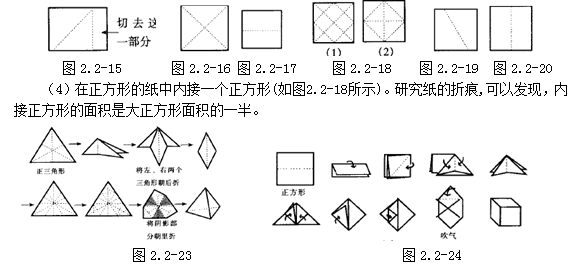
其实，我们还可以像图 2.2-25这样以正方形的角或中心为顶点，折出 60°或 30°角。即，在正方形纸片 ABFE中，先将对边 AE、 BF重合，折出折痕 DG；如图 2.2-25所示，过顶点 A，将边 AB向上对折，使得 B点刚好落在折痕 DG上，记为 O点。此时，∠ BAO、∠ EAO依次是 60°角、 30°角。

（ 11）将长方形纸片折成三等份大多数人将长方形纸片折成三等份的惯用方法是：

先从纸片的一边开始，估计地叠起纸片的三分之一；然后，将对边也折起来，根据三份是否重合来进行调整。

当然，这种折法蕴涵着朴素的极限思想；反复折叠中，一次比一次地更趋近三等份。 

另外一种完全不同的折法是：

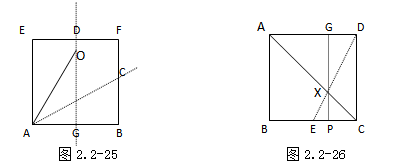
如图 2.2-26所示，先将整张纸片 ABCD的一条边 BC对折（使点 B、 C重合），找到其中点 E点；再折出整张纸片的对角线 AC，以及 E点与 D点的连线 ED，两条折痕相交于点 X；最后，过交点 X折叠纸片，使 DG重叠在 AG上、 CE重叠在 BE上。此时，则 DG即为 AG的三分之一。

利用边 BC与 AD平行以及 E点是中点可知⊿ CXE∽⊿ AXD，进而， AG： GD=AG： PC=AX： CX=AD： CE=CB： CE=2。显然，相似三角形的性质是这种折法的核心。