第二次数学危机--无穷小是零吗

【慕联导读】

18世纪，微分法和积分法在生产和实践上都有了广泛而成功的应用，大部分数学家对这一理论的可靠性是毫不怀疑的。

1734年，英国哲学家、大主教贝克莱发表《分析学家或者向一个不信正教数学家的进言》，矛头指向微积分的基础--无穷小的问题，提出了所谓贝克莱悖论。他指出：牛顿在求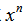的导数时，采取先给x以增量0，应用二项式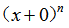，从中减去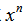以求得增量，并除以０以求出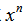的增量与x的增量之比，然后又让０消失，这样得出增量的最终比。这里牛顿做了违反矛盾律的手续──先设x有增量，又令增量为零，也即假设x没有增量。他认为无穷小dx既等于零又不等于零，召之即来，挥之即去，这是荒谬。无穷小量究竟是不是零？无穷小及其分析是否合理？由此而引起了数学界甚至哲学界长达一个半世纪的争论。导致了数学史上的第二次数学危机。 18世纪的数学思想的确是不严密的，直观的强调形式的计算而不管基础的可靠。其中特别是：没有清楚的无穷小概念，从而导数、微分、积分等概念也不清楚，无穷大概念不清楚，以及发散级数求和的任意性，符号的不严格使用，不考虑连续就进行微分，不考虑导数及积分的存在性以及函数可否展成幂级数等等。

直到19世纪20年代，一些数学家才比较关注于微积分的严格基础。从波尔查诺、阿贝尔、柯西、狄里赫利等人的工作开始，到威尔斯特拉斯、戴德金和康托的工作结束，中间经历了半个多世纪，基本上解决了矛盾，为数学分析奠定了严格的基础。

同学们对第二次数学危机---无穷小是零吗，可能还是不能够理解清楚，其实也没有太多的关系，随着我们之后的学习发展，相信同学们会慢慢理解体会的，现阶段，我们就把这个当成一个故事了解一下就可以了。数学危机的出现可以看出，数学的发展过程是艰辛曲折的，但是，古代的科学家刻苦专研的精神，为数学发展奠定了坚实的基础，也为我们树立了好的榜样。